The holiday season has begun, and with it, increased air travel. And just in time, the Wall Street Journal released an amazing study ranking the best US airports.
The article’s main conclusion is that San Francisco (SFO) is the best airport, followed by Atlanta (ATL), while among other large airports, Newark (EWR) can be found at the bottom of the list.
Well … I must disagree. I fly between Newark and SFO quite often, and personally, I like the first, and find the latter to be highly overrated. And if you’re a long-term reader, you know I care a lot about travel, and that I like being right. But I also like to think that I’m a rational, data-driven decision-maker.
So I went on a quest to prove the article wrong, and myself right.
Well, actually no…
This was not my main concern with the Wall Street Journal article. The article did an amazing job with collecting data on many different aspects regarding the service quality of various airports. Really amazing job:
“The Wall Street Journal ranked the 50 busiest airports based on 19 measures that span a journey, from ticket purchase through takeoff and landing. We divided the airports into two categories: the 20 largest airports, in terms of number of passengers, and the next 30 we call midsize; each group has distinct advantages and challenges.”
The study uses 19 factors that are divided into three broader categories, all clearly important to travelers: reliability, convenience, and value.
Reliability: (which according to the WSJ, got the highest score) includes factors such as on-time arrivals (measured as the percentage of flights that arrived at the gate less than 15 minutes after schedule), on-time departures (measured as the percentage of flights that departed the gate less than 15 minutes after schedule), and a few others.
Convenience: includes J.D. Powers customer satisfaction scores, the number of nonstop destinations, and average Yelp reviews of airport restaurants, and more.
Value: includes, among others, the average domestic fare from the airport, the UberX fare from the convention center to the airport, and the leading airline’s market share as a measure of competition at the airport.
Really admirable work of data collection and choice of factors. The WSJ then assigned weights to each metric and computed an overall score, based on which it ranked airports.
The “problem” with this ranking is that the choice of weights assigned to each metric matters because it can make a world of a difference. I’m sure I can find weights that will make every airport look good.
But, can I?
The Efficient Frontier
This brings me to my favorite method of conducting such rankings: the efficient frontier.
It’s necessary to find a way to allow weights to be assigned as objectively as possible, while acknowledging the tradeoffs between the different metrics —some airports excel at on-time performance, while others just offer better value in terms of tickets, etc.
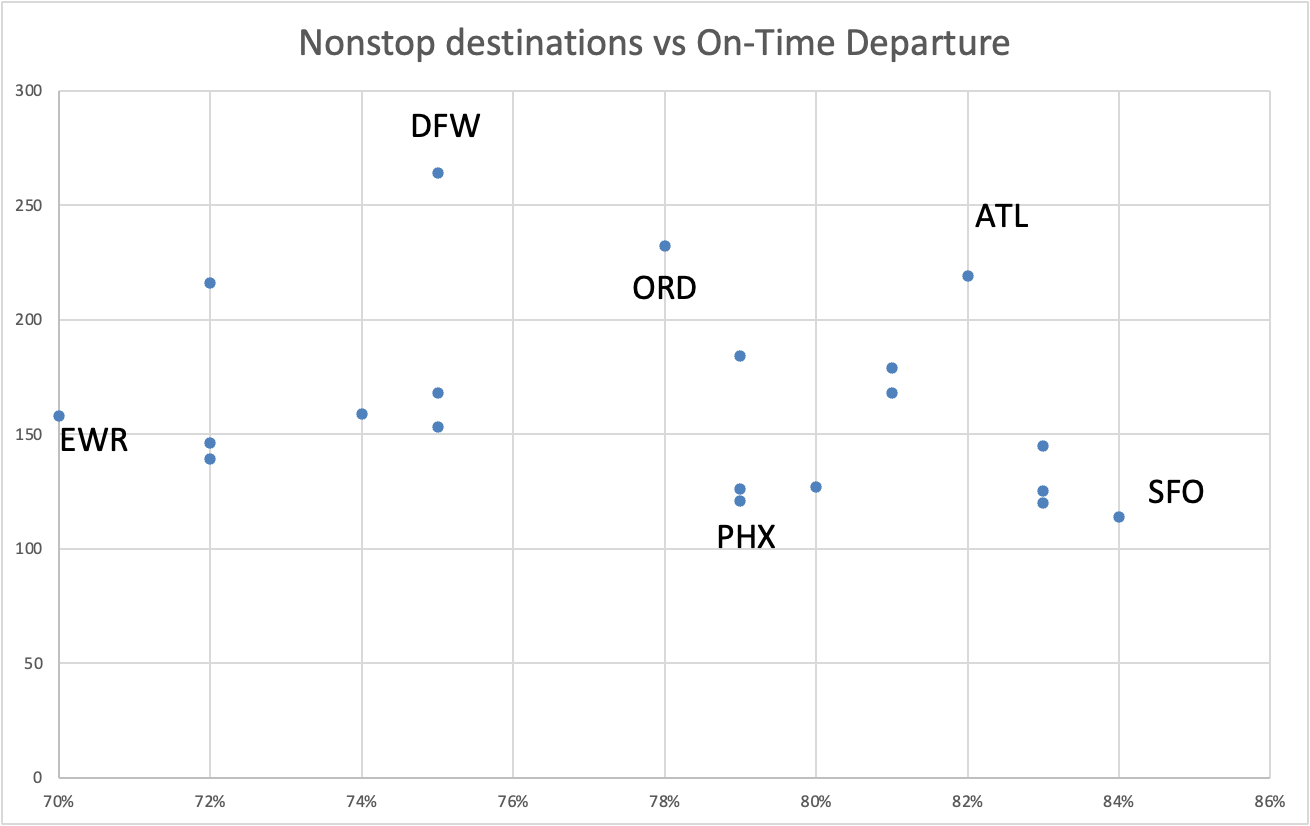
For example, the following graph shows various airports in terms of two metrics. The x-axis is the percentage of on-time departures and the y-axis is the number of locations that you can take a direct flight from each airport. As you can see, some airports (notably SFO) have great on-time departure, yet lack in terms of how many options there are for direct flights to and from the airport.
Other airports, such as Dallas/Fort Worth, have a massive number of direct flights, but they must compromise in terms of on-time departure, given the complexity of running the airports and the dependency between flights.
Yet, you can also see that some airports are just not very good. They don’t have many flights, and have terrible on-time departure statistics … Newark, for example.
The way to capture this tradeoff is by using the notion of the efficient frontier. It actually can be drawn nicely when looking at a two dimensional graph:
The line is the efficient frontier. It basically looks for the airports that are “best in class” in the following sense: To be on the frontier means that given the on-time departure, no other airport offers more direct flight locations, and given the number of locations they offer direct flights to, no other airport offers a better on-time departure. All other airports, that are not on the frontier, are just “dominated” by airports along both dimensions.
You may wonder, “Why these specific metrics?” …and you’re right. If I choose different metrics, such as number of direct flights and average domestic fare, it would result in a different “frontier”:
Using those metrics, Las Vegas airport offers many discounted fares (even if it lacks in terms of the number of direct flights), and DFW is rather expensive but offers many discounted flights.
If you wonder about the metric I am using (and why it is negative): I computed the average fares across all airports, and for each airport, I computed where it stands with respect to that average. Some airports have a negative value, which means they are more expensive than the average airport, while other airports have a positive value, which means that they are, on average, discounted when compared to other airports. Why? The frontier works well with metrics where the higher the level, the better the airport.
Note that on this frontier, SFO is expensive and offers limited options.
The remaining question is how can we calculate this in a way that accounts for more than two metrics (hence dimensions), yet keeps the idea of fairness?
The method I’ll use is called Data Envelopment Analysis (DEA).
DEA
First I’ll describe the method and how I used it to analyze the airline data where we want to have more than two metrics, and then we can try to understand the results.
The idea, which was first published in the seminal paper, Measuring the efficiency of decision-making units by Charnes, Cooper, and Rhodes, involves the use of linear programming to measure the relative efficiency of decision-making units.
So each airport is a “decision-making unit,” and its efficiency is measured as the ratio of the weighted sum of the metrics (I’m simplifying the method here).
How do you choose the weights? Here’s what makes this method so smart:
Let’s say we’re looking at SFO. We’re “telling” the airport to find the weights that will allow it to achieve the highest efficiency, bounded by 100%, but on one condition: after finding its best weights, when using the same weights, and given their own parameters, all other airports can’t be more than 100% efficient. In other words, we can’t make others be “super efficient” to make a single airport look “efficient.”
As per the immortal words, “if everybody is efficient, then no one is.”
The next step may sound very casual, but there’s a simple way to write it into a linear program and even run it in excel. The nice thing about this method is that it doesn’t suppose any weights or any parametric relationship between them.
It’s a great benchmarking method: if you are “efficient,” there is at least one metric (maybe all the weight is on one specific metric) you can excel in. If you are inefficient, someone’s doing a better job in generating better performance.
The method can be generalized, it’s very fair, and allows for combining different types of metrics without supposing any structure or relationship between them. Here, we focus only on “output” metrics and won’t account for factors one would consider as “inputs” (such as weather, investment, etc).
Unfortunately, one thing we lose when we have more dimensions is the ability to visualize, so no more nice graphs.
Applying DEA to Airport Efficiency
An important step here is to choose which metrics to look at. With the DEA method, when there are too many metrics, almost all airports will look efficient, so we must choose a limited number.
I chose four metrics:
On-time departure as a metric of reliability.
Number of locations with a direct flight as a measure of convenience.
The average domestic fare, and the average Uber price to the nearest convention center as measures of value.
Notes: I’m not making any assumptions about what people prefer. I experimented with a few other metrics (e.g., maximum walking distance, price of water, average Yelp rating), but there wasn’t a big impact on the results, and I also removed “customer satisfaction” since I wanted to include only objective measures.
As we’ve seen already, there is no single airport that dominates all others. If there was, it would be the only one on the “efficiency” line.
The Results
First, the table:
The first thing to note is that there are several “efficient” airports (in green):
Large airports: San Francisco (SFO) , Atlanta (ATL), Minneapolis (MSP), Phoenix (PHX) , Las Vegas (LAS), Charlotte (CLT) , Denver (DEN) , Chicago O'Hare (ORD) , Dallas/Fort Worth (DFW).
Smaller airports: Fort Lauderdale (FLL) , San Diego (SAN), San Jose (SJC) , Portland (PDX) , Honolulu (HNL) Salt Lake City (SLC) and Oakland (OAK).
Note that these are exactly some of the airports that we came across in the two-dimensional efficient frontier graph. They’re not great, but given the combination of these factors, other airports are not doing a much better job. For example, SLC's proximity to the city (and the slopes, which I’m not considering here), and high on-time-departure makes it an excellent airport. Note that SFO and ATL, which were at the top of the WSJ ranking, are also included. But here is the thing: I didn’t choose them ... the data did.
Then we have the “pretty good airports” (in yellow). These are airports that are not efficient. This means that there really are no weights that can make them look efficient, but they are 95%-99% of the way to becoming efficient.
Some surprising names there: Detroit (DTW), Los Angeles (LAX), New York LaGuardia (LGA), Houston Bush (IAH), Boston (BOS), and Philadelphia (PHL).
And then we have those that are really not good.
The five worst airports in the US (in red) are: New York JFK (JFK), Newark (EWR), Dallas Love (DAL) Chicago Midway (MDW), and Baltimore (BWI).
What makes them so bad? Newark, for example, is expensive, far from the city (expensive UberX), and among the worst in terms of delays.
So the WSJ was right, and I was wrong.
But this brings me to another important issue: Your choice of airport depends on many factors.
I like Newark because it connects well to Philly through Amtrak (something I’ve written about in the past). I’m not interested in the distance to the nearest convention center, and I need an airport that flies to specific destinations (many of which are not offered directly from PHL). While SFO is great, I don’t live nearby.
But this list may inform you of your choices if you are planning a layover somewhere or a holiday trip and you want a location with a convenient airport.
And for the upcoming holiday, in case you haven’t booked anything yet, I hope this list helps you make the right choices (or at the very least, helps you impress others at the office holiday party).





beyond price we really need a metric for how inconvenient it is to exit an airport via Uber. The LAXit experience is so horrible that I would heavily knock off from its convenience score because of it. 😂
This part sounds intuitively like the idea of comparative advantage, but are they as closely related mathematically as my intuition suggests?: "It’s a great benchmarking method: if you are “efficient,” there is at least one metric (maybe all the weight is on one specific metric) you can excel in. if you are inefficient, someone’s doing a better job in generating better performance. "