Sky’s the Limit: Unraveling the Economics of All-You-Can-Fly Passes

Recently, more and more airlines are offering annual passes where you pay a fee upfront and you can book seats, given available capacity. The most interesting and highly discussed pass is offered by Frontier Airlines:

“The pass is called GoWild and it allows passengers the chance to hop on any domestic or international Frontier flight. I bought the $1,999 annual pass for $600 during a limited-time 48-hour sale. While it may seem great, there are some caveats you should be aware of.”

The idea of all-you-can-fly airline passes isn’t new. In fact, a few years ago, American Airlines realized that, when unlimited, these passes can be extremely costly.

The rules around the Frontier Airline passes are quite stringent. For domestic travel, flights must be booked 24 hours before departure, which eliminates the option of scheduling a trip ahead of time. For international travel, bookings must be made 10 days in advance. Round trips are excluded, so travelers either book their return flight 24 hours before their desired departure date (risking availability), or book a regular return flight (at the usually increased “last-miute” rate). Additional fees for carry-on and checked baggage apply, with costs varying by flight date, while taxes, often around $30, are also not included.

The airline is also rethinking its general pricing:

“According to the airline, the new monthly pass is a spinoff of the GoWild! All-You-Can-Fly Fall and Winter Pass which allows unlimited travel from Sept. 2, 2023 - Feb. 29, 2024 for $299.”

A WSJ journalist tried the pass, and reports: 

“I put the pass to the test, playing nine days of Frontier flight roulette in late June. The total cost for seven flights: $673.21 in taxes and fees on top of the original pass.”

Her conclusion: 

“It all worked out. But for a business trip next week, I won’t be using my Frontier pass.”

There are several complaints: An NBC News article details the frustration of Denise Smith, a San Francisco Bay Area resident with the pass. Mrs. Smith, a frequent traveler, was initially delighted by Frontier Airlines’ GoWild pass, a three-month all-you-can-fly package for $699, allowing domestic and international flights. Starting strong with five trips in April and May, her excitement waned as June approached, when she suddenly couldn’t find flights. In their response, Frontier emphasized that the GoWild pass is tailored for those with great flexibility like retirees and remote workers. 

The article also quotes Jacob Brown, a Denver teacher and GoWild expert, who moderates a Facebook group for pass holders, sharing tips and insights. He’s observed varying opinions on the pass, with some calling it the “best thing they’ve ever done” and others deeming it a scam. Brown explained that GoWild members access leftover seats at low cost and that availability can be tight, especially in peak seasons. “‘It really is unlimited access to empty seats,’ he noted, ‘but it’s also summer... so it’s going to be difficult to use the pass if you’re trying to go somewhere that everyone else is trying to go to.’”

So who is right? Are these unlimited passes a good idea? If so, at what price? 

As usual, the answer is not so simple, so let’s take a closer look. 

The Airline’s POV

With the new promotions, it’s clear Frontier is trying to entice more people to buy the pass. 

So, what does the airline’s math reveal?

Generally, the best way to depict how airlines think about their pricing and seat availability is by using the newsvendor formula —airlines call it Littlewood’s rule (potato-potahto). 

Imagine two types of travelers with different willingness to pay: leisure and business.

Leisure travelers have a low willingness to pay (we’ll use PL) and thus want to book in advance. Business travelers have a higher willingness to pay and need to maintain flexibility as they don’t always know which flight they’ll take. For simplicity, let’s assume the airline needs to decide on how many seats to keep available for last-minute business travelers, who would be willing to pay. Let’s assume business travelers are willing to pay PB> PL. 

The overage cost is a seat that isn’t used for business or leisure. So the cost is PL (assuming you can fill the entire plane at this price). 

Underage cost: PB-PL (the cost of a seat that was demanded but unavailable since a leisure customer has already booked it). 

So, using the newsvendor formula, the optimal Service Level is: 

SL = (PB-PL)/(PB-PL+PL) = (PB- PL)/PL. 

If PL= 150, and PB = 500, then SL = (500-150)/500 = 70%. 

It’s important to note that this doesn’t mean keeping 70% of the plane available, but rather: the number of seats that need to be allocated to business passengers should be able to accommodate all demand “scenarios” of business travelers 70% of the time. 

This, of course, is a simplified example. In reality, travelers don’t announce their “type,” and not all business passengers are the same, etc., but this is a good starting point. 

How will this change with the GoWild pass? Well, GoWild passengers can only book a day before, so they only have access to “last-minute” available seats, and don’t bring any additional revenue. In contrast, they may prevent actual paying passengers from booking. 

So, on the single-flight level, this doesn’t change the math of how many seats are held for business, etc.

However, one can look at it very cynically: The pass just offers net revenues to the airline. Customers pay upfront and can only use it if the flight is almost empty. So the airline collects  money upfront without the obligation to reserve any seats. 

Not so simple!

What’s the tradeoff?

When the load factor (a term used to describe airlines’ utilization) is high, flights are almost full, so GoWild passengers can’t prevent paying passengers from booking seats and the airline actually profits from the pass. Sounds great for the airline right?. 

But what happens when the load factor is very high? In that case, the likelihood of a GoWild passenger finding a seat is very low, and if they do, they’re most likely preventing a paying customer from booking a seat. So, maybe it’s not that great for the airline, after all. The odds are that the pass works better during the off-peak season when the load factor is low. 

But this is no longer a simple newsvendor model. 

Maybe we need to boil it down to the question: What should the price of the pass be, given the airline’s load factor (which will undoubtedly change if more people buy the pass)? 

To better understand this, let’s move to the customer side. 

The Passenger’s POV

If you’re a frequent traveler, you’ve likely encountered intriguing offers like the GoWild pass with tantalizing promises of unlimited flights. But before taking to the skies, there’s a series of questions to ponder. What’s the likelihood of securing the flights you desire? How does availability shift with the load factor or time frame? How much are customers truly willing to utilize such a service? This dance between demand and availability is a complex one, where the more people participate, the less advantageous it may become for others, and vice versa. 

Let’s delve into these questions.

What does the passenger’s math reveal? 

When passengers buy the pass, they’re hoping to make the most of it. But using it depends on the likelihood of space availability in the 24-hour period leading up to their desired flight. This availability depends on the anticipated load factor (which dictates how full the plane will be), and the number of passengers using the pass (which increases competition). 

A one-year GoWild pass costs $2,000. Assuming a frequent flyer does one flight per week, that’s enough to generate $40 savings off the pass, so it’s worth it. 

To make things a bit more concrete, and given that the analytics is not simple, and given that I don’t think anyone really studied this problem, I decided to run simulations to understand the problem better. 

An important note: The code and graphs were generated using the ChatGPT Code Interpreter. I reviewed the code, and it seems correct, but I leave a small possibility for error. If there is a mistake, it’s mine for not catching it. 

Second note: this newsletter officially “jumped the shark,” if this newsletter post is almost an academic paper. 

A final note: I’m not claiming the following numbers are correct or representative of all routes and all people, but this simulation gives us a glimpse into the main tradeoffs. 

Calculations were based on the following parameters, which are reduced to a single flight for simplicity:

• Plane Capacity: 100 seats

• Regular Ticket Price: $500

• Arrival Rate: 4.5 passengers/day

• Number of Days Passengers Start Booking Seats Before the Flight: 20

• Price of All-You-Can-Fly Pass: $40/week

• Additional Pay per Flight for Pass Holders: $0 (this is meant for simplicity and can be absorbed into the regular price as taxes and other fees are excluded). 

• Number of Customers (that buy the pass and may be relevant for this flight): 1,000 

• Theta (θ): Percentage of customers that pay for the all-you-can-fly pass.

• Lambda (λ): Percentage of customers that pay for the all-you-can-fly pass and try to buy tickets for the flight in the final 24 hours (e.g., 10%)

The first simulation computes and plots the likelihood of finding a seat for All-You-Can-Fly passengers as a function of θ for the specified arrival rates (4.6, 4.7, 4.8, 4.9, and 5 customers per day). Each arrival rate will be represented by a different color on the graph. Each arrival rate stands for a different fill rate (4.5 customers per day, without the pass will bring us to a 90% load factor). 

According to the graph, the likelihood of finding a seat decreases with the % of passengers who have the pass (as expected) and decreases very rapidly with the demand for the specific flight. So, if demand for the flight has an equal number of paying passengers and pass holders, even with a load factor of about 90%, the likelihood of getting a ticket is below 10%. 

So you pay $40 for a “weekly pass,” but can only utilize it 10% of the time. If this is the case, you will travel only five times a year, and on these flights, you will save $500 dollars, which means you’re still better off, but barely. 

The next graph shows similar results regarding how often people try to utilize the pass. As the % increases, as expected, the likelihood of finding a ticket decreases. 

So the fact that people are complaining is no surprise. As more people get the pass, finding a ticket during peak season (with a high load factor) will become increasingly difficult.

Back to the Airline

So how much should the airline charge for the pass? 

For varying arrival rates (from 4.5 to 5 per day which proxy for different load factors), with θ fixed at 5% and λ at 10%, the breakeven price for the All-You-Can-Fly pass is the price at which the revenue from selling the passes equals the lost revenue from regular ticket sales that couldn’t find a seat in the last 24 hours. 

I (and by “I,” I mean my Chatty “intern”) ran the simulation with the following steps:

• Calculated the lost revenue for each arrival rate.

• Calculated the revenue from selling passes.

• Determined the breakeven price for the pass where the revenue from passes equals the lost revenue.

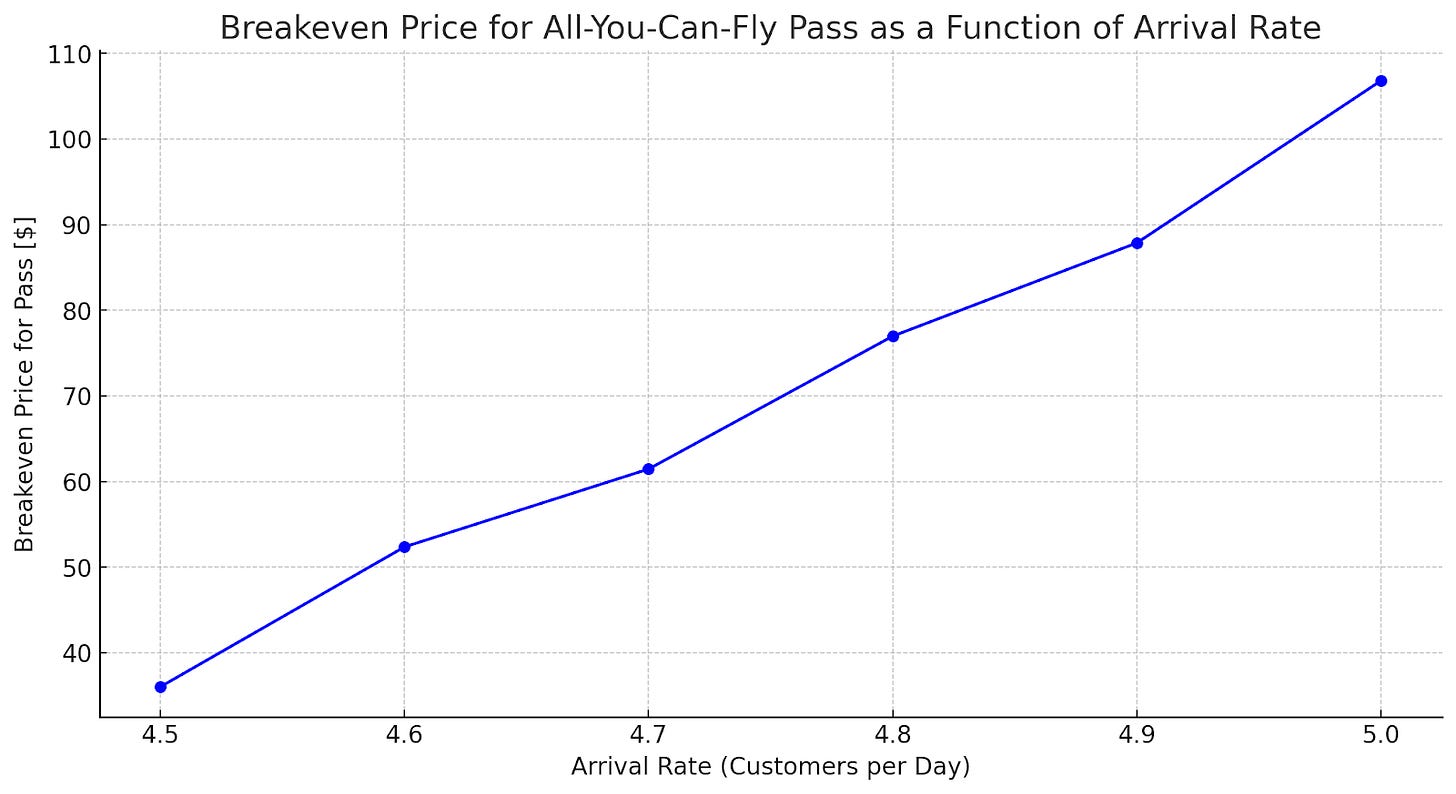
The following graph shows the breakeven price for the All-You-Can-Fly passes as a function of the arrival rate, ranging from 4.5 to 5 customers per day. 

As we can see, the breakeven price increases with the arrival rate, reflecting the increased opportunity cost of selling the All-You-Can-Fly passes instead of regular tickets. The interesting aspect is that as the load factor increases, the airline needs to make enough money to justify the potential loss of revenues from these passengers. While counterintuitive, it makes sense: as the number of seats becomes tighter, the airline is not willing to give these empty seats (which may reduce the likelihood of a paying passenger) unless they are paying enough for it. 

What’s the passengers’ willingness to pay? 

The passenger’s breakeven price for the pass can be calculated as follows:

Passenger’s Breakeven Price for the annual pass= Regular Ticket Price × Likelihood of Finding a Seat × Number of Weeks.

As the arrival rate increases, and with it, the load factor, the likelihood of finding a ticket becomes lower, which is reflected in a lower willingness to pay (very intuitive): 

Now let’s combine the passenger and airline graphs. Since both graphs have different directions, there might not always be an equilibrium. For an equilibrium to exist, there should be enough people willing to pay, at a reasonable price set by the airline. 

Let’s see when that can happen:

Here’s the plot showing the range of available equilibria for the All-You-Can-Fly pass as a function of the arrival rate (passengers per day). The plot includes:

• The passengers’ weekly breakeven price (in green), which represents the price at which passengers are indifferent between purchasing the pass and buying regular tickets.

• The Airline’s breakeven price (in blue), which represents the price at which the airline is indifferent between selling and not selling the pass.

The shaded region (to the left of the crossing point) represents the range of available equilibria where both the airline and the passengers are indifferent. To the right of the meeting point, the airline must charge more than the passenger’s breakeven price, which means they won’t buy the pass. 

So there’s only a narrow set of load factor values (below 92%) where it makes sense to purchase a pass. The reason I say narrow is that in 2023, the average load factor is 85%, which means that at least half the year, the load factor is higher, and during the holiday seasons, it’s usually above 90%. 

Does this mean passengers should avoid purchasing the pass altogether? The answer is that I don’t know. A decision like this depends on numerous factors unknown to me and the airline (at least for now). 

For instance, to make such a determination, you need to know how demand will change (that is, theta), which is difficult, so I leave it at this. If you are a doctoral student or faculty interested in working on this (or aware of a paper that solves it), let me know! 

My final conclusion is that this idea can be an interesting value promotion for retirees and remote workers that can heavily utilize the pass when traveling off-season. It’s also a good way for airlines to increase their utilization during their off-season when planes are emptier. So maybe they shouldn’t be selling it at an annual or even quarterly level, but as a low-season pass. However, as more people return to the office for work, I believe the market for such a pass will shrink even further.